Як шукати невизначений інтеграл. Невизначений інтеграл

Знайти невизначений інтеграл (безліч первісних або "антипохідних") означає відновити функцію за відомою похідною цієї функції. Відновлена ​​безліч первісних F(x) + З для функції f(x) враховує константу інтегрування C. За швидкістю переміщення матеріальної точки (похідної) то, можливо відновлено закон руху цієї точки (первообразная); щодо прискорення руху точки - її швидкість та закон руху. Як бачимо, інтегрування - широке полі діяльності Шерлоков Холмсов від фізики. Та й в економіці багато понять надаються через функції та їх похідні і тому, наприклад, можна за продуктивністю праці у певний момент часу (похідної) відновити обсяг продукції, випущений у відповідний час.

Щоб знайти невизначений інтеграл, потрібна досить невелика кількість основних формул інтегрування. Але процес його знаходження значно важче, ніж лише застосування цих формул. Вся складність відноситься не до інтегрування, а до приведення інтегрованого виразу до такого виду, який дає можливість знайти невизначений інтеграл за вищезазначеними основними формулами. Це означає, що для початку практики інтегрування потрібно активізувати набуті в середній школі навички перетворення виразів.

Вчитися знаходити інтеграли будемо, користуючись властивостями та таблицею невизначених інтегралівз уроку про основні поняття цієї теми (відкриється у новому вікні).

Існує кілька методів знаходження інтеграла, з яких метод заміни змінноїі метод інтегрування частинами- обов'язковий джентльменський набір кожного, хто успішно здав найвищу математику. Однак починати освоювати інтегрування корисніше і приємніше із застосуванням методу розкладання, заснованому на двох теоремах про властивості невизначеного інтеграла, які для зручності повторимо тут.

Теорема 3.Постійний множник у подинтегральном вираженні можна виносити за знак невизначеного інтеграла, тобто.

Теорема 4.Невизначений інтеграл суми алгебри кінцевого числа функцій дорівнює сумі алгебри невизначених інтегралів цих функцій, тобто.

(2)

Крім того, в інтегруванні може стати в нагоді наступне правило: якщо вираз підінтегральної функції містить постійний множник, то вираз первісної домножується на число, зворотне постійному множнику, тобто

(3)

Оскільки цей урок - вступний у вирішення завдань інтегрування, важливо відзначити дві речі, які або вже на початковому етапі, або трохи пізніше можуть вас здивувати. Здивування пов'язане з тим фактом, що інтегрування - операція, зворотна диференціюванню і невизначений інтеграл можна справедливо називати "антипохідною".

Перша річ, якою не слід дивуватися при інтегруванні.У таблиці інтегралів існують формули, які не мають аналогів серед формул похідної таблиці . Це такі формули:

Однак можна переконатися в тому, що похідні виразів, що стоять у правих частинах цих формул, збігаються з відповідними підінтегральними функціями.

Друга річ, якій не слід дивуватися при інтегруванні. Хоча похідна будь-якої елементарної функції є також елементарною функцією, невизначені інтеграли від деяких елементарних функцій вже не є елементарними функціями . Прикладами таких інтегралів можуть бути такі:

Для вироблення техніки інтегрування стануть у нагоді такі навички: скорочення дробів, розподіл багаточлена в чисельнику дробу на одночлен у знаменнику (для отримання суми невизначених інтегралів), перетворення коренів у ступені, множення одночлена на багаточлен, зведення в ступінь. Ці навички потрібні для перетворень підінтегрального виразу, у яких має вийти сума інтегралів, присутніх у таблиці інтегралів.

Знаходимо невизначені інтеграли разом

приклад 1.Знайти невизначений інтеграл

.

Рішення. Бачимо у знаменнику підінтегрального виразу багаточлен, у якому ікс у квадраті. Це майже вірна ознака того, що можна застосувати табличний інтеграл 21 (з арктангенсом у результаті). Виносимо із знаменника множник-двійку (є така властивість інтеграла - постійний множник можна виносити за знак інтеграла, вище воно було згадано як теорема 3). Результат всього цього:

Тепер у знаменнику є сума квадратів, а це означає, що можемо застосувати згаданий табличний інтеграл. Остаточно отримуємо відповідь:

.

приклад 2.Знайти невизначений інтеграл

Рішення. Знову застосовуємо теорему 3 - властивість інтеграла, на підставі якого постійний множник можна виносити за знак інтеграла:

Застосовуємо формулу 7 з таблиці інтегралів (змінна до ступеня) до підінтегральної функції:

.

Скорочуємо дроби і перед нами кінцева відповідь:

приклад 3.Знайти невизначений інтеграл

Рішення. Застосовуючи спочатку теорему 4, а потім теорему 3 про властивості знайдемо даний інтеграл як суму трьох інтегралів:

Усі три отримані інтеграли – табличні. Використовуємо формулу (7) з таблиці інтегралів при n = 1/2, n= 2 і n= 1/5, і тоді

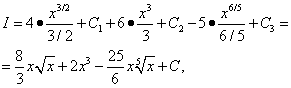
поєднує всі три довільні постійні, які були запроваджені при знаходженні трьох інтегралів. Тому в аналогічних ситуаціях слід запроваджувати лише одну довільну постійну (константу) інтегрування.

приклад 4.Знайти невизначений інтеграл

Рішення. Коли знаменнику подинтегральной дробу - одночлен, можемо почленно розділити чисельник на знаменник. Вихідний інтеграл перетворився на суму двох інтегралів:

.

Щоб застосувати табличний інтеграл, перетворимо коріння в міру і ось вже остаточна відповідь:

Продовжуємо знаходити невизначені інтеграли разом

Приклад 7.Знайти невизначений інтеграл

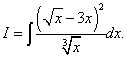
Рішення. Якщо ми перетворимо підінтегральну функцію, звівши двочлен у квадрат і розділивши почленно чисельник на знаменник, то вихідний інтеграл стане сумою трьох інтегралів.

Вирішення інтегралів. Розповідаємо, як вирішувати інтеграли.

Інтеграл - розширене математичне поняття суми. Рішення інтегралівабо їхнє знаходження називається інтегруванням. Користуючись інтегралом, можна знайти такі величини, як площа, обсяг, масу та інше. Рішення інтегралів(Інтегрування) є операція зворотна диференціювання. Щоб краще уявляти, що є інтеграл, представимо його у наступній формі. Уявіть. У нас є тіло, але поки не можемо описати його, ми тільки знаємо, які у нього елементарні частинки і як вони розташовані. Для того, щоб зібрати тіло в єдине ціле, необхідно проінтегрувати його елементарні частинки - злити частини в єдину систему. У геометричному вигляді для функції y=f(x), інтеграл являє собою площу фігури обмеженою кривою, віссю х, і двома вертикальними лініями х=а і х=b.

Так ось площа зафарбованої області є інтеграл від функції в межах від a до b. Не віриться? Перевіримо на будь-які функції. Візьмемо найпростішу у=3. Обмежимо функцію значення а=1 і b=2. Побудуємо: Отже, обмежена фігура прямокутник. Площа прямокутника дорівнює добутку довжини на ширину. У нашому випадку довжина 3, ширина 1, площа 3*1=3. Спробуємо вирішити теж не вдаючись до побудови, використовуючи інтегрування: Як бачите відповідь вийшла та сама. Рішення інтегралів - це збирання в жодних елементарних елементів. У випадку з площею сумуються смужки дуже малої ширини. Інтеграли можуть бути певними та невизначеними. Вирішити певний інтеграл означає визначити значення функції у заданих межах. Рішення невизначеного інтеграла зводитись до знаходження первісної. F(x) – первісна. Диференціюючи першорядну, ми отримаємо вихідний підінтегральний вираз. Щоб перевірити, чи правильно ми вирішили інтеграл, ми диференціюємо отриману відповідь і порівнюємо з вихідним виразом. Основні функції та первісні для них наведені в таблиці:

Таблиця первісних на вирішення інтегралів

Основні прийоми рішення інтегралів: Вирішити інтеграл, значить проінтегрувати функцію змінної. Якщо інтеграл має табличний вигляд, можна сказати, що, як вирішити інтеграл, вирішено. Якщо ж ні, то основним завданням при вирішенні інтеграла ставати зведення його до табличного виду. Спочатку слід запам'ятати основні властивості інтегралів:

Знання цих основ дозволить вирішувати прості інтеграли. Але слід розуміти, що більшість інтегралів складні і для їх вирішення необхідно вдатися до використання додаткових прийомів. Нижче розглянемо основні приклади рішення інтегралів. Прийоми будуть надані для загального ознайомлення без прикладів рішення, щоб не перевантажувати статтю Потрібно розуміти, що за 5 хвилин прочитання статті вирішувати всі складні інтеграли ви не навчитеся, але правильно сформований каркас розуміння дозволить заощадити години часу на навчання та вироблення навичок за рішенням інтегралів.

Основні прийоми вирішення інтегралів

1. Заміна змінної.
Для виконання даного прийому знадобиться хороша навичка знаходження похідних.

2. Інтегруванняпо частинах. Користуються такою формулою. Застосування цієї формули дозволяє начебто нерозв'язні інтеграли привести до рішення.

3. Інтегруваннядробово-раціональних функцій. - розкласти дріб на найпростіші - Виділити повний квадрат. - Створити в чисельнику диференціал знаменника.

4. Інтегруваннядробово-ірраціональних функцій. - Виділити під коренем повний квадрат - Створити в чисельнику диференціал підкореного виведення. 5. Інтегрування тригонометричних функцій. При інтегруванні виразів виду застосовує формули розкладання добутку. Для виразів m-непарне, n-будь-яке, створюємо d(cosx). Використовуємо тотожність sin 2 +cos 2 =1 m,n – парні, sin 2 x=(1-cos2x)/2 та cos 2 x=(1+cos2x)/2 Для виразів виду: - Застосовуємо властивість tg 2 x=1/cos 2 x – 1

1. Розібратися в суті інтегралів. Необхідно зрозуміти базову сутність інтеграла та його рішення. Інтеграл насправді є сума елементарних елементів об'єкта інтегрування. Якщо йдеться про інтегрування функції, то інтеграл є площа фігури між графіком функції, віссю х та межами інтегрування. Якщо інтеграл невизначений, тобто межі інтегрування не вказані, то рішення зводитись до знаходження первісної. Якщо інтеграл певний, необхідно підставити значення кордонів у знайдену функцію. 2. Відпрацювати використання таблиці первісних і основних властивостей інтегралів. Необхідно навчитися користуватися таблицею первісних. За безліччю функцій першорядні знайдені та занесені до таблиці. Якщо ми маємо інтеграл, які є у таблиці, можна сказати, що його вирішено. 3. Розібратися у прийомах та напрацювати навички рішення інтегралів.Якщо інтеграла не табличного виду, його рішення зводитися до приведення його до виду одного з табличних інтегралів. Для цього ми використовуємо основні властивості та прийоми рішення. У разі, якщо на якихось етапах застосування прийомів у вас виникають труднощі та нерозуміння, то ви детальніше знаєтеся саме на цьому прийомі, дивіться приклади подібного плану, запитуєте у викладача. Додатково після рішення інтегралуна перших етапах рекомендується звіряти рішення. Для цього ми диференціюємо отриманий вираз та порівнюємо з вихідним інтегралом. Відпрацюємо основні моменти на кількох прикладах:

Приклади вирішення інтегралів

Приклад 1: Розв'язати інтеграл: Інтеграл невизначений. Знаходимо первісну. І тому інтеграл суми розкладемо у сумі інтегралів. Кожен із інтегралів табличного виду. Дивимося первісні за таблицею. Рішення інтеграла: Перевіримо рішення (знайдемо похідну).

Почнемо вивчення теми « Невизначений інтеграл», і навіть докладно розберемо приклади рішень найпростіших (і зовсім) інтегралів. Як завжди, ми обмежимося мінімумом теорії, яка є у численних підручниках, наше завдання – навчитися вирішувати інтеграли.

Що потрібно знати для успішного освоєння матеріалу? Для того, щоб впоратися з інтегральним обчисленням, Вам необхідно вміти знаходити похідні щонайменше на середньому рівні. Чи не зайвим досвідом буде, якщо у Вас за плечима кілька десятків, а краще – сотня самостійно знайдених похідних. Принаймні, Вас не повинні ставити в глухий кут завдання на диференціювання найпростіших і найпоширеніших функцій.

Здавалося б, причому тут взагалі похідні, якщо мова у статті піде про інтеграли?! А справа ось у чому. Справа в тому, що знаходження похідних і знаходження невизначених інтегралів (диференціювання та інтегрування) – це дві взаємно зворотні дії, як, наприклад, складання/віднімання або множення/розподіл. Таким чином, без навички і будь-якого досвіду знаходження похідних, на жаль, далі не просунутися.

У цьому нам знадобляться такі методичні матеріали: Таблиця похіднихі Таблиця інтегралів.

У чому складність вивчення невизначених інтегралів? Якщо похідних мають місце суворо 5 правил диференціювання, таблиця похідних і досить чіткий алгоритм дій, то інтегралах все інакше. Існують десятки способів та прийомів інтегрування. І, якщо спосіб інтегрування спочатку підібраний невірно (тобто. Ви не знаєте, як вирішувати), то інтеграл можна «колоти» буквально цілодобово, як справжнісінький ребус, намагаючись помітити різні прийоми і хитрощі. Декому навіть подобається.

Між іншим, нам досить часто доводилося чути від студентів (не гуманітарних спеціальностей) думку на кшталт: «У мене ніколи не було інтересу вирішити межу чи похідну, але ось інтеграли – зовсім інша справа, це цікаво, завжди є бажання «зламати» складний інтеграл» . Стоп. Вистачить чорного гумору, переходимо до цих невизначених інтегралів.

Якщо методів рішення існує багато, то з чого почати вивчення невизначених інтегралів чайнику? В інтегральному численні існують, на наш погляд, три стовпи або своєрідна «вісь», навколо якої обертається решта. Насамперед слід добре розібратися у найпростіших інтегралах (ця стаття).

Потім потрібно детально опрацювати урок. ЦЕ ВАЖЛИВИЙ ПРИЙОМ! Можливо, навіть найважливіша стаття з усіх статей, присвячених інтегралам. І, по-третє, обов'язково слід ознайомитися з методом інтегрування частинами, оскільки з допомогою нього інтегрується великий клас функций. Якщо Ви опануєте хоча б ці три уроки, то вже не два. Вам можуть «вибачити» незнання інтегралів від тригонометричних функцій, інтегралів від дробів, інтегралів від дрібно-раціональних функцій, інтегралів від ірраціональних функцій (коренів)Але якщо «сісти в калюжу» на методі заміни або методі інтегрування частинами – то це буде дуже і дуже погано.

Отже, починаємо із простого. Погляньмо на таблицю інтегралів. Як і похідних, ми помічаємо кілька правил інтегрування та таблицю інтегралів від деяких елементарних функцій. Будь-який табличний інтеграл (та й взагалі будь-який невизначений інтеграл) має вигляд:

Відразу розуміємося на позначеннях і термінах:

- Значок інтеграла.

- Підінтегральна функція (пишається з літерою "и").

- Диференціал значок. Що це таке, ми розглянемо дуже скоро. Головне, що при записі інтеграла і в ході рішення важливо не втрачати значок. Помітний недолік буде.

- Підінтегральний вираз або "начинка" інтеграла.

– первіснафункція.

– . Не потрібно сильно завантажуватися термінами, тут найважливіше, що у будь-якому невизначеному інтегралі до відповіді приплюсовується константа .

Вирішити невизначений інтеграл – це означає знайтибезліч первісних функційвід цієї підінтегральної функції

Ще раз подивимося на запис:

Подивимося на таблицю інтегралів.

Що відбувається? Ліві частини у нас перетворюютьсядо інших функцій: .

Спростимо наше визначення:

Вирішити невизначений інтеграл - Це означає перетворити його на невизначену (з точністю до константи) функцію , користуючись деякими правилами, прийомами та таблицею.

Візьмемо, наприклад, табличний інтеграл . Що сталося? Символічний запис перетворився на безліч першорядних функцій.

Як і у випадку з похідними, для того щоб навчитися знаходити інтеграли, не обов'язково бути в курсі, що таке інтеграл, або першорядна функція з теоретичної точки зору. Достатньо просто здійснювати перетворення за деякими формальними правилами. Так, у випадку зовсім не обов'язково розуміти, чому інтеграл перетворюється саме на . Можна прийняти цю та інші формули як даність. Усі користуються електрикою, але мало хто замислюється, як там по дротах бігають електрони.

Так як диференціювання та інтегрування - протилежні операції, то для будь-якої первісної, яка знайдена правильно, справедливо наступне:

Іншими словами, якщо продиференціювати правильну відповідь, то обов'язково має вийти вихідна підінтегральна функція.

Повернемося до того ж табличного інтегралу .

Переконаємося у справедливості цієї формули. Беремо похідну від правої частини:

- Це вихідна підінтегральна функція.

Ось, до речі, стало зрозуміліше, чому до функції завжди приписується константа. При диференціюванні константа завжди перетворюється на нуль.

Вирішити невизначений інтеграл– це означає знайти безліч всіхпервісних, а не якусь одну функцію. У табличному прикладі , , , і т. д. - всі ці функції є рішенням інтеграла . Рішень нескінченно багато, тому записують коротко:

Таким чином будь-який невизначений інтеграл досить легко перевірити. Це деяка компенсація за велику кількість інтегралів різних видів.

Переходимо до розгляду конкретних прикладів. Почнемо, як і щодо похідної, з двох правил інтегрування:

- Константу Cможна (і треба) винести за знак інтегралу.

- Інтеграл суми (різниці) двох функцій дорівнює сумі (різниці) двох інтегралів. Це правило справедливе для будь-якої кількості доданків.

Як бачите, правила, в принципі, такі самі, як і для похідних. Іноді їх називають властивостями лінійностіінтеграл.

Приклад 1

Знайти невизначений інтеграл.

.

Виконати перевірку.

Рішення:Найзручніше перетворити його, як.

(1) Застосовуємо правило . На забуваємо записати значок диференціала dxпід кожним інтегралом. Чому під кожним? dx- Це повноцінний множник.Якщо розписувати детально, перший крок слід записати так:

.

(2) Відповідно до правила виносимо всі константи за знаки інтегралів. Зверніть увагу, що в останньому доданку tg 5 – це константа, її також виносимо.

Крім того, на цьому кроці готуємо коріння та ступеня для інтегрування. Так само, як і при диференціюванні, коріння треба подати у вигляді . Коріння та ступеня, які розташовуються у знаменнику – перенести вгору.

Примітка:на відміну від похідних, коріння в інтегралах далеко не завжди слід приводити до вигляду а ступеня переносити вгору.

Наприклад, – це готовий табличний інтеграл, який уже порахували до Вас, і всякі китайські хитрощі на кшталт зовсім не потрібні. Аналогічно: - Це теж табличний інтеграл, немає ніякого сенсу представляти дріб у вигляді . Уважно вивчіть таблицю!

(3) Усі інтеграли у нас табличні. Здійснюємо перетворення за допомогою таблиці, використовуючи формули: , і

для статечної функції - .

Слід зазначити, що табличний інтеграл – це окремий випадок формули для статечної функції: .

Константу C достатньо приплюсувати один раз наприкінці виразу

(а не ставити їх після кожного інтегралу).

(4) Записуємо отриманий результат у більш компактному вигляді, коли всі ступені виду

знову представляємо у вигляді коріння, а ступеня з негативним показником скидаємо назад у знаменник.

Перевірка. Для того щоб виконати перевірку, потрібно продиференціювати отриману відповідь:

Отримано вихідну підінтегральна функція, Т. е. Інтеграл знайдено правильно. Від чого танцювали, до того й повернулися. Добре, коли історія з інтегралом закінчується саме так.

Іноді трапляється трохи інший підхід до перевірки невизначеного інтеграла, коли від відповіді береться не похідна, а диференціал:

.

У результаті отримуємо не підінтегральну функцію, а підінтегральний вираз.

Не варто лякатися поняття диференціал.

Диференціал - це похідна, помножена на dx.

Однак нам важливі не теоретичні тонкощі, а те, що з цим диференціалом робити далі. Диференціал розкривається так: значок d прибираємо, праворуч над дужкою ставимо штрих, наприкінці виразу приписуємо множник dx :

Отримано вихідне підінтегральний виразтобто інтеграл знайдено правильно.

Як бачите, диференціал зводиться до знаходження похідної. Другий спосіб перевірки мені подобається менше, тому що доводиться додатково малювати великі дужки та тягнути піктограму диференціала dx остаточно перевірки. Хоча він коректніший, або «солідніший», чи що.

Насправді можна було промовчати про другий спосіб перевірки. Справа не в способі, а в тому, що ми навчилися розкривати диференціал. Ще раз.

Диференціал розкривається так:

1) значок dприбираємо;

2) праворуч над дужкою ставимо штрих (позначення похідної);

3) наприкінці виразу приписуємо множник dx .

Наприклад:

Запам'ятайте це. Розглянутий прийом знадобиться дуже скоро.

Приклад 2

.

Коли ми знаходимо невизначений інтеграл, то ЗАВЖДИ намагаємося зробити перевірку, тим більше, для цього є чудова нагода. Не всі типи завдань у вищій математиці є подарунком з цього погляду. Неважливо, що часто контрольні завдання перевірки не потребують, її ніхто, і ніщо не заважає провести на чернетці. Виняток можна зробити лише тоді, коли не вистачає часу (наприклад, на заліку, екзамені). Особисто я завжди перевіряю інтеграли, а відсутність перевірки вважаю халтурою та неякісно виконаним завданням.

Приклад 3

Знайти невизначений інтеграл:

. Виконати перевірку.

Рішення: Аналізуючи інтеграл, ми бачимо, що у нас під інтегралом добуток двох функцій, та ще й зведення у ступінь цілого вираження. На жаль, на терені інтегральної битви ніхороших та зручних формул для інтегрування твору та приватногоу вигляді: або .

Тому, коли дано твір чи приватний, завжди має сенс подивитися, а чи не можна перетворити підінтегральну функцію на суму? Розглянутий приклад - той випадок, коли можна.

Спочатку наведемо повне рішення, коментарі будуть нижчими.

Отримано вихідну підінтегральна функція, Отже, інтеграл знайдено правильно.

Під час перевірки функцію завжди бажано «упакувати» до первісного виду, виносячи, у разі, за дужки і застосовуючи формулу скороченого множення у напрямі: .

Приклад 4

Знайти невизначений інтеграл

Виконати перевірку.

Це приклад самостійно рішення. Відповідь та повне рішення наприкінці уроку.

Приклад 5

Знайти невизначений інтеграл

. Виконати перевірку.

У цьому прикладі підінтегральна функція є дріб. Коли ми бачимо в підінтегральному вираженні дріб, то першою думкою має бути питання: «А чи не можна якось від цього дробу позбутися, або хоча б його спростити?».

Помічаємо, що у знаменнику знаходиться самотнє коріння з «ікс». Один у полі – не воїн, отже, можна почленно розділити чисельник на знаменник:

Дії з дробовими ступенями ми не коментуємо, оскільки про них неодноразово йшлося у статтях про похідну функцію.

Якщо Вас таки ставить у глухий кут такий приклад, як

і ні в яку не виходить правильна відповідь,

Також зверніть увагу, що у рішенні пропущено один крок, а саме застосування правил , . Зазвичай за певного досвіду рішення інтегралів ці правила вважають очевидним фактом і не розписують докладно.

Приклад 6

Знайти невизначений інтеграл. Виконати перевірку.

Це приклад самостійно рішення. Відповідь та повне рішення наприкінці уроку.

У загальному випадку з дробами в інтегралах не все так просто, додатковий матеріал з інтегрування дробів деяких видів можна знайти у статті: Інтегрування деяких дробів. Але, перш ніж перейти до вищезгаданої статті, необхідно ознайомитися з уроком: Метод заміни у невизначеному інтегралі. Справа в тому, що підведення функції під диференціал або метод заміни змінної є ключовим моментому вивченні теми, оскільки зустрічається не лише «у чистих завданнях на метод заміни», а й у багатьох інших різновидах інтегралів.

Рішення та відповіді:

Приклад 2: Рішення:

Приклад 4: Рішення:

У цьому прикладі ми використовували формулу скороченого множення

Приклад 6: Рішення:

Інтеграли онлайн на сайт для закріплення студентами та школярами пройденого матеріалу. Щоразу, як тільки почати вирішувати інтеграл, потрібно виявити його тип, без цього не можна застосовувати жоден метод, якщо не вважати його табличним. Не всякий табличний інтеграл видно явно із заданого прикладу, іноді потрібно перетворити вихідну функцію, щоб знайти первісну. Насправді рішення інтегралів зводиться до інтерпретування завдання з знаходження вихідної, тобто первісної з нескінченного сімейства функцій, але якщо задані межі інтегрування, то за формулою Ньютона-Лейбніца залишається лише одна єдина функція, до якої потрібно застосовувати розрахунки. Неформально інтеграл онлайн є площею між графіком функції та віссю абсцис у межах інтегрування. Дозвольте нам обчислити складний інтеграл по одній змінній та пов'язати його відповідь із подальшим вирішенням завдання. Можна, що мовиться, в лоб знайти його від підінтегральної функції. Відповідно до основної теореми аналізу, інтегрування є операцією, зворотної диференціювання, чим допомагає вирішувати диференціальні рівняння. Існує кілька різних визначень операції інтегрування, що відрізняються у технічних деталях. Проте всі вони сумісні, тобто будь-які два способи інтегрування, якщо їх можна застосувати до цієї функції, дадуть той самий результат. Найпростішим є інтеграл Рімана – це певний інтеграл чи невизначений інтеграл. Неформально integral однією змінною можна запровадити як площі під графіка (фігури, укладеної між графіком функції та віссю абсцис). Намагаючись знайти цю площу, можна розглядати фігури, що складаються з певної кількості вертикальних прямокутників, основи яких складають разом відрізок інтегрування і виходять при розбитті відрізка на кількість маленьких відрізків. Калькулятор вирішує інтеграли з описом дій докладно та безкоштовно! Невизначений інтеграл онлайн для функції – це сукупність всіх первісних цієї функції. Якщо функція визначена і безперервна на проміжку, то для неї є первісна функція (чи сімейство первісних). Краще ретельно підійти до цієї справи та випробувати внутрішнє задоволення від виконаної роботи. Але обчислити інтеграл спосіб відмінний від класичного, часом призводить до несподіваних результатів і дивуватися цьому не можна. Тішить той факт, який надасть позитивний резонанс на те, що відбувається. Список певних інтегралів та невизначених інтегралів з повним докладним покроковим рішенням. Знаходження невизначеного інтеграла онлайн є дуже частою задачею у вищій математиці та інших технічних розділах науки. Основні методи інтегрування. Подумайте про виконані будівлі раніше, ніж знайдуться помилки. Рішення інтегралів онлайн – ви отримаєте докладне рішення для різних типів інтегралів: невизначених, певних, невласних. Інтеграл функції – аналог суми послідовності. Неформально кажучи, певний інтеграл є частиною графіка функції. Найчастіше такий інтеграл визначає, наскільки тіло важче порівнюваного з ним об'єкта такої ж щільності, і неважливо, якої він форми, тому що поверхня не вбирає воду. Як знайти інтеграл онлайн знає кожен студент молодших курсів На базі шкільної програми цей розділ математики також вивчається, але не докладно, а лише ази такої складної та важливої ​​теми. Найчастіше студенти приступають до вивчення інтегралів з великої теорії, якій передують теж важливі теми, такі як похідна і граничні переходи - вони межі. Рішення інтегралів поступово починається з найелементарніших прикладів від простих функцій і завершується застосуванням безлічі підходів і правил, запропонованих ще в минулому столітті і навіть набагато раніше. Інтегральне обчислення має ознайомлювальний характер у ліцеях і школах, тобто у середніх навчальних закладах. Наш сайт сайт завжди допоможе вам і рішення інтегралів онлайн стане для вас звичайним, а найголовніше зрозумілим заняттям. На базі даного ресурсу ви легко зможете досягти досконалості в цьому математичному розділі. Осягаючи крок за кроком досліджувані правила, наприклад, такі як інтегрування, частинами або застосування методу Чебишева, ви легко вирішите на максимальну кількість балів будь-який тест. То як же нам обчислити інтеграл, застосовуючи відому всім таблицю інтегралів, але так, щоб рішення було правильною, коректною і з максимально можливою точною відповіддю? Як навчитися цьому та чи можливо це зробити звичайному першокурснику у найкоротший термін? На це запитання відповімо ствердно – можна! При цьому ви не тільки зможете вирішити будь-який приклад, але й досягнете висококласного рівня інженера. Секрет простий як ніколи – необхідно докласти максимального зусилля, приділити необхідну кількість часу на самопідготовку. На жаль, ще ніхто не вигадав іншого способу! Але не все так хмарно, як здається на перший погляд. Якщо ви звернетеся до нашого сервісу сайт з даним питанням, то ми полегшимо вам життя, тому що наш сайт може обчислювати інтеграли онлайн докладно, при цьому з дуже високою швидкістю та бездоганно точною відповіддю. По суті інтеграл не визначає, як впливає ставлення аргументів на стійкість системи загалом. Механічний зміст інтеграла полягає у багатьох прикладних завданнях, це визначення обсягу тіл, і обчислення маси тіла. Потрійні та подвійні інтеграли беруть участь якраз у цих розрахунках. Ми наполягаємо на тому, щоб рішення інтегралів онлайн проводилося тільки під наглядом досвідчених викладачів і через численні перевірки. Ми відповідаємо, що студенти народ вільний і можуть проходити навчання екстерном, готуючись до заліку чи екзамену в комфортних домашніх умовах. За лічені секунди наш сервіс допоможе кожному бажаючому обчислити інтеграл від будь-якої заданої функції змінної. Перевірити отриманий результат слід взяттям похідної від первинної функції. При цьому константа від рішення інтеграла звертається до нуля. Це правило очевидно для всіх. Існує не багато таких сайтів, які за лічені секунди видають покрокову відповідь, а головне з високою точністю та у зручному вигляді. Але не слід забувати і про те, як є можливість знайти інтеграл за допомогою готового сервісу, перевіреного часом і випробуваного на тисячах вирішених прикладів у режимі онлайн.

Калькулятор вирішує інтеграли з описом дій ДЕТАЛЬНО російською мовою та безкоштовно!

Рішення невизначених інтегралів

Це онлайн сервіс у один крок:

Рішення певних інтегралів

Це онлайн сервіс у один крок:

• Ввести підінтегральний вираз (підінтегральну функцію)
• Ввести нижню межу для інтегралу
• Ввести верхню межу для інтегралу

Рішення подвійних інтегралів

• Ввести підінтегральний вираз (підінтегральну функцію)

Рішення невласних інтегралів

• Ввести підінтегральний вираз (підінтегральну функцію)
• Введіть верхню область інтегрування (або нескінченність)
• Ввести нижню область інтегрування (або - нескінченність)

Рішення потрійних інтегралів

• Ввести підінтегральний вираз (підінтегральну функцію)
• Ввести нижню та верхню межі для першої області інтегрування
• Ввести нижню та верхню межу для другої області інтегрування
• Ввести нижню та верхню межу для третьої області інтегрування

Даний сервіс дозволяє перевірити свої обчисленняна правильність

Можливості

• Підтримка всіх можливих математичних функцій: синус, косинус, експонента, тангенс, котангенс, корінь квадратний та кубічний, ступеня, показові та інші.
• Є приклади для введення, як невизначених інтегралів, так невласних і певних.
• Виправляє помилки у ведених виразах і пропонує свої варіанти для введення.
• Чисельне рішення для певних та невласних інтегралів (у тому числі для подвійних та потрійних інтегралів).
• Підтримка комплексних чисел, а також різних параметрів (ви можете вказувати в підінтегральному вираженні не тільки змінну інтеграцію, а й інші змінні параметри)